8 (応用例)ポアソン方程式 直接法

8.1 概要

今回は，ポアソン方程式を直接法で解きます．

8.2 アルゴリズムの解説

1次のポアソン方程式の一般系を

$$\frac{d^2\phi }{dx^2}=\rho$$

と書くとします．この時，2次精度の差分式は，

$$\frac{\phi _{j-1}-2\phi _j+\phi _{j+1}}{\Delta x^2}=\rho _j$$

となります．
そして，$\phi _1=0$と$\phi _N=0$が境界条件として与えられた時，

$$\begin{bmatrix} -2 & 1 & & & & & \ 1 & -2 & 1 & & & & \ & ... ...ts\ \rho _j\ \vdots\ \rho _{N-2}\ \rho _{N-1} \end{array} \right)$$

というAx=y型の方程式を解けば，分布$\phi$が求められます． より詳しい解説は他を御覧下さい．

8.3 例題

$$\frac{d^2\phi }{dx^2}=-k^2\mathrm{sin}(kx) (k=2\pi )$$

を解く．但し，境界条件を $\phi (0)=0$, $\phi (1)=0$とし， $0\leq x \leq 1$の範囲で201個に離散化する．


コードを以下に示します．

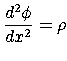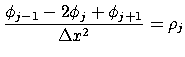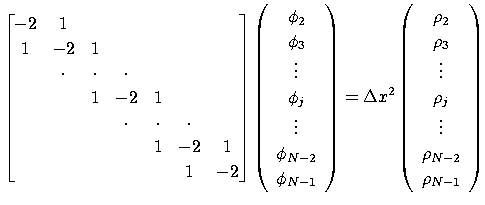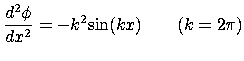//====================================================================[include]
#include ``cpplapack.h''

//=======================================================================[main]
/*! main */
int main(int argc, char** argv)
{
  //// declare objects ////
  const int N(201);
  const double dx(1/(double)(N-1));
  const double k(2*MPI);
  CPPL::dgbmatrix A(N-2,N-2,1,1);
  CPPL::dcovector rho(N-2);

  //// make dgbmatrix A ////
  A.identity();
  A *= -2;
  for(int i=0; i<A.n-1; i++){
    A(i,i+1) = 1;
    A(i+1,i) = 1;
  }

  //// make dcovector rho ////
  for(int i=0; i<rho.l; i++){
    rho(i) = -k*k*sin((i+1)*k*dx);
  }
  rho *= dx*dx;

  //// solve A*phi=dx^2*rho ////
  A.dgbsv(rho);

  //// print ////
  std::cout << ``x       phi(x)      Ans'' << std::endl;
  std::cout << ``0 0 0'' << std::endl;
  for(int i=0; i<rho.l; i++){
    std::cout << (i+1)*dx << `` `` << rho(i) << `` `` << sin((i+1)*k*dx) 
              << std::endl;
  }
  std::cout << ``1 0 0'' << std::endl;

}

実行結果は以下の様になります．

x       phi(x)      解析解
0 0 0
0.005 0.0314133 0.0314108
0.01 0.0627957 0.0627905
0.015 0.0941161 0.0941083
0.02 0.125344 0.125333
0.025 0.156447 0.156434
0.03 0.187397 0.187381
0.035 0.218161 0.218143
0.04 0.24871 0.24869
0.045 0.279014 0.278991
0.05 0.309042 0.309017
0.055 0.338766 0.338738
0.06 0.368155 0.368124
0.065 0.397181 0.397148
0.07 0.425814 0.425779
0.075 0.454028 0.45399
0.08 0.481793 0.481754
0.085 0.509083 0.509041
0.09 0.535871 0.535827
0.095 0.56213 0.562083
0.1 0.587834 0.587785
0.105 0.612957 0.612907
0.11 0.637476 0.637424
0.115 0.661366 0.661312
0.12 0.684603 0.684547

$\vdots$