7 (応用例)離散複素フーリエ変換

7.1 概要

二つめの例は離散複素フーリエ変換です．

7.2 アルゴリズムの解説

離散フーリエ変換の定義式は次のようになります．

$$X_k=\sum_{n=0}^{N-1} x_n e^{-j\frac{2 \pi kn}{N}}$$

そこで，

$$W=e^{-j\frac{2 \pi }{N}}$$

とし，

$$\begin{bmatrix} W^0 & W^0 & W^0 & \cdots & W^0\ W^0 & W^1 & W... ...gin{array}{c} X_0\ X_1\ X_2\ \vdots\ X_{N-1} \end{array} \right)$$

というAx=y型の方程式を解けば，n次の離散フーリエ変換を求められます． より詳しい解説は他を御覧下さい．

7.3 例題

data.txtから離散データを読み込み，10次のフーリエ変換をしてdft.txtに出力する．


コードを以下に示します．

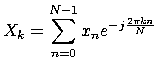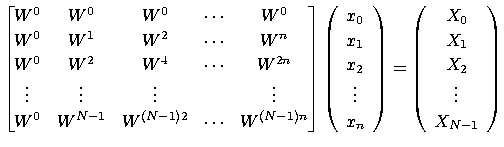//====================================================================[include]
#include ``cpplapack.h''

//========================================================================[DFT]
void DFT(CPPL::zcovector& X, int n)
{
  //// make zgematrix A ////
  CPPL::zgematrix A(X.l,n+1);
  for(int i=0; i<A.m; i++){ for(int j=0; j<A.n; j++){
    A(i,j) = std::complex<double>(std::cos((i*j)*2*MPI/(X.l))
                                ,-std::sin((i*j)*2*MPI/(X.l)));
  }}

  //// solve Ax=X ////
  A.zgels(X);
}

//=======================================================================[main]
/*! main */
int main(int argc, char** argv)
{
  //// make zcovector X ////
  CPPL::zcovector X;
  X.read(``data.txt'');

  //// solve ////
  DFT(X,10);

  //// write ////
  X.write(``dft.txt'');

  return 0;
}

data.txtの中身です．

zcovector 100
(1,3.97901e-10)
(0.998027,-0.0627905)
(0.992115,-0.125333)
(0.982287,-0.187381)
(0.968583,-0.24869)
(0.951057,-0.309017)
(0.929776,-0.368125)
(0.904827,-0.425779)
(0.876307,-0.481754)
(0.844328,-0.535827)

$\vdots$

dft.txtの中身です．

zcovector 11
(2.07977e-07,6.53992e-09)
(1,-6.4705e-07)
(-2.07977e-07,6.54019e-09)
(-1.03885e-07,6.54021e-09)
(-6.91412e-08,6.5401e-09)
(-2.80132e-08,6.53977e-09)
(-4.12676e-08,6.54009e-09)
(-3.42625e-08,6.54017e-09)
(-2.92385e-08,6.54009e-09)
(-3.86341e-08,6.53992e-09)
(-2.24983e-08,6.54008e-09)

]