5 (基本演算)特異値分解

5.1 概要

CPPLapackでは，特異値分解を行うための関数が各行列クラスのメンバ関数として用意されています．

      dgematrix.dgesvd
      zgematrix.zgesvd

5.2 使い方

ここではdouble型の実一般行列を例に紹介します．
行列Aの特異値分解を行うには下記の様に記述します．AはM行N列行列です．

      A.dgesvd(S,U,VT);

Sは特異値を出力するdcovector型，Uは左特異ベクトル，VTは右特異ベクトルを出力するdgematrix型です．

5.3 注意点

計算後，行列Aは上書きされてしまいます．元の値を保持したい場合は，関数を呼び出す前にコピーを作っておいて下さい．

5.4 例題

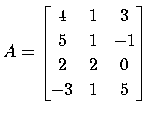行列 $A= \begin{bmatrix} 4 & 1 & 3 \\ 5 & 1 & -1\\ 2 & 2 & 0 \\ -3 & 1 & 5 \\ \end{bmatrix}$ を特異値分解する．


コードを以下に示します．

//====================================================================[include]
#include ``cpplapack.h''

//=======================================================================[main]
/*! main */
int main(int argc, char** argv)
{
  //// make dgematrix A  ////
  CPPL::dgematrix A(4,3);
  A(0,0)=4;  A(0,1)=1;  A(0,2)=3;
  A(1,0)=5;  A(1,1)=1;  A(1,2)=-1;
  A(2,0)=2;  A(2,1)=2;  A(2,2)=0;
  A(3,0)=-3; A(3,1)=1;  A(3,2)=5;

  //// make S, U and VT ////
  CPPL::dcovector S;
  CPPL::dgematrix U, VT;

  //// SVD A ////
  A.dgesvd(S,U,VT);

  //// print S, U, and VT ////
  std::cout << ``S=\n'' << S << std::endl;
  std::cout << ``U=\n'' << U << std::endl;
  std::cout << ``VT=\n'' << VT << std::endl;

  return 0;
}

実行結果は以下の様になります．

S=
 7.61305
 5.94552
 1.64083

U=
 -0.404476 -0.672423 0.445651 -0.430862
 -0.678796 -0.0902972 -0.0493761 0.727079
 -0.287353 -0.181365 -0.872916 -0.350075
 0.541353 -0.711899 -0.192289 0.403933

VT=
 -0.947144 -0.146673 0.285317
 -0.230125 -0.309031 -0.922791
 0.22352 -0.939674 0.258944