4 (基本演算)固有値問題

4.1 概要

CPPLapackでは，固有値問題を解くための関数が各行列クラスのメンバ関数として用意されています．

      dgematrix.dgeev
      dgematrix.dggev
      dsymatrix.dsyev
      zgematrix.zgeev
      zgematrix.zggev
      zsymatrix.zsyev

4.2 使い方

ここではdouble型の実一般行列を例に紹介します．
正方行列Aの固有値を求めるには，以下の様にします．

      A.dgeev(wr,wi);

ここで，wr,wiは固有値の実部と虚部を出力するdouble型ベクトルコンテナです．
同時に右固有値と右固有ベクトルを求めたい時は，dcovector型ベクトルコンテナ， vrr,vriを用意して，

      A.dgeev(wr,wi,vrr,vri);

と記述します．
左固有値と左固有ベクトルを求めたい時は，drovector型ベクトルコンテナ，vlr,vliを用意して，

      A.dgeev(wr,wi,vli,vri);

と記述します． また，一般化固有値，一般化固有ベクトルが欲しい場合は，dggevを利用してください．

4.3 注意点

計算後，行列Aは上書きされてしまいます．元の値を保持したい場合は，関数を呼び出す前にコピーを作っておいて下さい．

4.4 例題

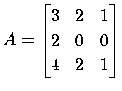行列 $A= \begin{bmatrix} 3 & 2 & 1 \\ 2 & 0 & 0 \\ 4 & 2 & 1 \\ \end{bmatrix}$ の固有値，固有ベクトルを求める．



コードを以下に示します．

//====================================================================[include]
#include ``cpplapack.h''

//=======================================================================[main]
/*! main */
int main(int argc, char** argv)
{
  //// make dgematrix A  ////
  CPPL::dgematrix A(3,3);
  A(0,0)=3; A(0,1)=2; A(0,2)=1;
  A(1,0)=2; A(1,1)=0; A(1,2)=0;
  A(2,0)=4; A(2,1)=2; A(2,2)=1;

  //// make wr wi vr ////
  std::vector<double> wr, wi;
  std::vector<CPPL::dcovector> vrr, vri;

  //// dgeev ////
  A.dgeev(wr, wi ,vrr, vri);

  //// print ////
  for(int i=0; i<3; i++){
    std::cout << ``#### `` << i << ``th eigen ####'' << std::endl;
    std::cout << ``wr='' << wr[i] << std::endl;
    std::cout << ``wi='' << wi[i] << std::endl;
    std::cout << ``vrr=\n'' << vrr[i] << std::endl;
    std::cout << ``vri=\n'' << vri[i] << std::endl;
  }
}

実行結果は以下の様になります．

#### 0th eigen ####
wr=5
wi=0
vrr=
 0.620174
 0.248069
 0.744208

vri=
 0
 0
 0

#### 1th eigen ####
wr=-1
wi=0
vrr=
 0.447214
 -0.894427
 1.23361e-16

vri=
 0
 0
 0

#### 2th eigen ####
wr=1.36434e-16
wi=0
vrr=
 -5.22952e-17
 -0.447214
 0.894427

vri=
 0
 0
 0